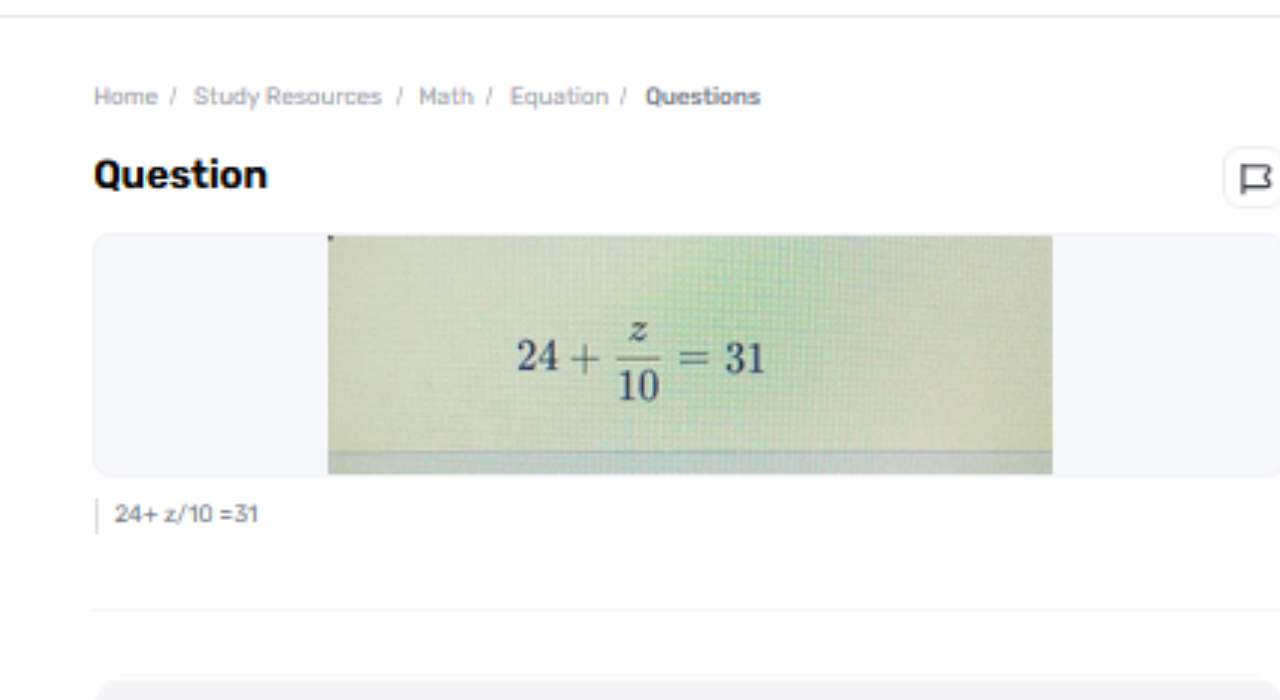
Solving conditions could be essential expertise in polynomial math that makes a difference in understanding how distinctive amounts relate to each other. The condition 24+10z=31 gives a commonsense case of how to isolate a variable and decide its esteem. In this article, we'll systematically solve for zzz by taking after an arrangement of arithmetical steps, guaranteeing that each portion of the method is obvious and comprehensible.
Understanding the Condition
The condition 24+10z=31 may be straight in one variable. This sort of condition speaks to a straight line when charted on a facilitated plane. The objective is to discover the esteem of zzz that produces the condition true. To do this, we have to isolate zzz on one side of the condition. This includes performing operations that rearrange the condition and illuminate the variable.
Segregating the Variable
To separate z, we to begin with have to kill the steady term on the side of the condition where zzz shows up. Within the given condition, 24 is included in 10z To evacuate this steady, we subtract 24 from both sides of the condition: 24+10z−24=31−24Streamlining both sides, we get: 10z=710z This step evacuates the consistent term from the cleared-out side of the condition, clearing out us with 10z alone on one side and a disentangled number on the other.
Tackling for the Variable With the condition presently disentangled to 10z=710z, we have to solve for zzz. Since zzz is duplicated by 10, we are going to partition both sides of the condition by 101010 separate z 10z10=710frac{10z}{10} Disentangling, we discover: z=710z = frac{7}{10}z=107 This result gives us the esteem of zzz that fulfills the initial condition.
Confirming the Arrangement
To guarantee that our arrangement is redress, we substitute z=710z = frac{7}{10}z=107 back into the first equation and confirm that both sides rise to: Substitute 710frac{7}{10}107 for zzz within the unique condition:24+10(710)=3124 + 10 left(frac{7}{10}right) = 31+10(107)=31 Perform the duplication:24+7=3124 + 7 = 3124+7=31 Include the numbers: 31=31 Since both sides of the condition are break even, our arrangement is confirmed as rectified.
Steps for Utilizing Gauth to Total Homework
Yield Your Address
To begin utilizing Gauth for homework help, input your particular address into the stage. You have the choice to either sort out the address or transfer any related records that might give extra settings. It's significant to be as point-by-point and clear as conceivable in your accommodation to guarantee you get exact and compelling back. Gauth will analyze your input to supply a custom-made reaction, leveraging its capabilities to address your particular needs and convey the foremost pertinent offer assistance.
Look at Arrangements and Experiences
Once Gauth forms your address, it'll offer comprehensive answers and point-by-point experiences. Take the time to thoroughly review these reactions to get the problem-solving methods and ideas used. The clarifications given are planned to assist you get a handle on the basic standards and methods, which can enhance your capacity to handle comparative issues in the future. By carefully considering these solutions, you'll pick up a more profound understanding of the fabric and improve your problem-solving aptitudes.
Hone and Assess Your Comprehension
To advance and strengthen your understanding, make utilize of Gauth intelligent instruments, such as tests and extra hone issues. Locks in with these features permits you to test your information and solidify your get a handle on of the concepts. On the off chance that you experience challenges, allude back to Gauth's supplementary clarifications and assets. This iterative handle guarantees you've got an exhaustive understanding before completing your homework, helping you to certainly apply what you learned.
Conclusion
In conclusion, tackling the condition 24+10z=31 includes confining the variable z to begin with evacuating the consistent term and after that isolating by the coefficient of z. Through these steps, we decided that z=710z = frac{7}{10}z=107. Confirming the arrangement affirms that our result is precise. This handle outlines key arithmetical methods and fortifies the significance of checking arrangements to guarantee rightness.